LEC 06
Q-table은 입력의 크기가 큰 실생활 예제에서는 적용이 어렵다.
퍼즐 80*80 pixel + 2color(black/white) => pow(2,80*80)만 해도 수가 엄청나게 크기에 table로 표현하기가 힘들다.
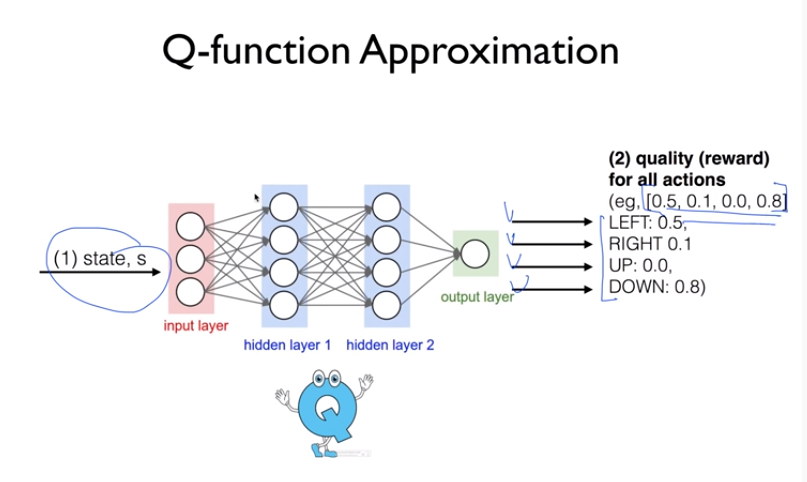
따라서, Q-Network, 신경망을 사용하여 Q 테이블을 근사한다.
Q-network, 신경망 구축은 '상태'만 input으로 주고 모든 가능한 행동의 확률값을 output으로 받는다.
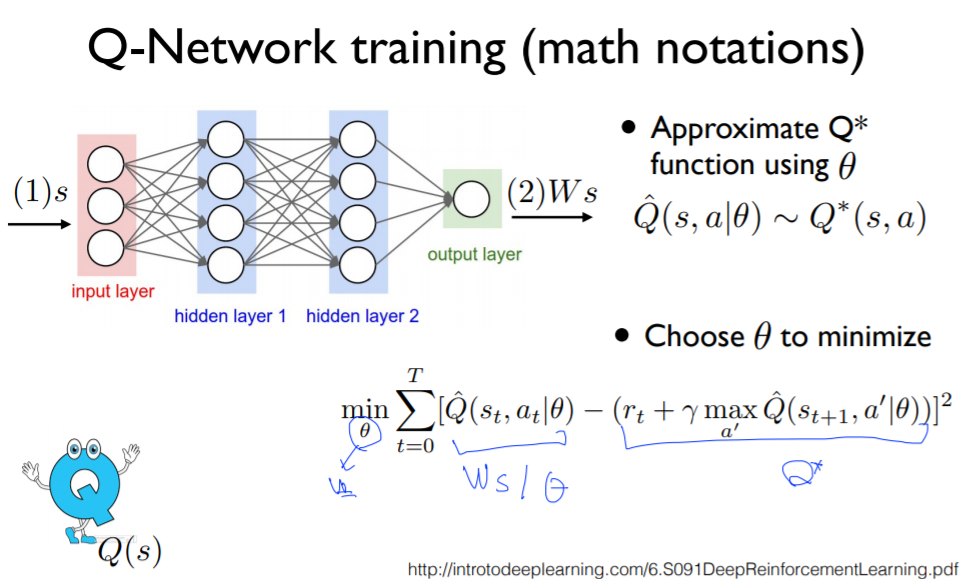
다음, Linear Regression 방식으로 문제를 해결한다.
1) 신경망 예측값 = 입력 s에 대해서 weights(W)를 적용한 출력값 -> W*s
2) 실제 목표 target, label = optimal Q => (reward + dis*max(Q(s',a'))
이제, loss function을 통해 위 2개값의 차이 제곱합이 최소가 되는 weights(W)를 구한다.
슬라이드에서는 조건부 확률을 사용하여, θ일때(특정 W) 현위치 s, 액현 a에서의 Q값으로 표현하였다.

전체적인 알고리즘은 에피소드 M번을 반복하는데, 처음 얻는 state에서는 전처리 과정을 거친다.
이후, E-greedy알고리즘으로 액션을 선택한다. { 액션a = 랜덤 or 가장 높은 큐 값 }
선택한 액션에 대해 환경env로 부터 다음 state와 reward을 돌려받고, 이 값으로 label값을 계산한다.
이때, label(y)는 terminal(도착지점)여부에 따라 구분가능하다. 도착지점에서는 다음 큐값이 없기에 reward만으로 y를 설정한다. ( FrozenLake의 경우)
그리고, gradient descent 방식으로 학습시킨다.

앞선 강의에서 deterministic과 stochastic 상황을 나누어 Q값을 다르게 구하였다.
stochastic상황에서는 멘토를 적게 믿어라!라는 교훈아래에 learning rate로 비중을 조절하여 계산하였다.
하지만, linear regression을 사용할 땐, 그럴 필요가 없다. 신경망에서는 상관하지 않기에 간단한 것을 채택한다.

하지만, 신경망에서는 테이블과 다르게 Q값이 수렴하지 않는다. -> DQN 다음 강의에서 자세히 다룰 예정이다.
LAB 06
Frozen Lake Q network
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
|
import gym
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
from keras import optimizers
def one_hot(x):
return np.identity(16)[x:x+1]
env = gym.make('FrozenLake-v0')
learning_Rate = 0.1
input_size = env.observation_space.n
output_size = env.action_space.n
dis = .99
num_episodes = 2000
model = tf.keras.Sequential([
tf.keras.layers.Dense(output_size, input_shape = [input_size],
kernel_initializer=tf.random_uniform_initializer(minval=0, maxval=0.01))
])
model.compile(optimizers.SGD(learning_rate = learning_rate), loss = 'mse')
print(model.summary())
with tf.device('/GPU:0'):
rList = []
for i in range(num_episodes):
s = env.reset()
e = 1.0/ ((i/50)+10)
rAll = 0
done = False
local_loss = []
while not done:
Qs = model.predict(one_hot(s))
if np.random.rand(1) < e:
a = env.action_space.sample()
else:
a = np.argmax(Qs)
s1, reward, done, _ = env.step(a)
if done:
Qs[0,a] = reward
else:
Qs1 = model.predict(one_hot(s1))
Qs[0,a] = reward + dis * np.argmax(Qs1)
model.fit(x = one_hot(s), y = Qs)
rAll += reward
s = s1
rList.append(rAll)
print("Percent of successful episode:" + str(sum(rList)/num_episodes) + '%')
plt.bar(range(len(rList)), rList, color='blue')
plt.show()
|
cs |
Car Pole Q network
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
|
import gym
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
env = gym.make('CartPole-v0')
learning_rate = 1e-1
input_size = env.observation_space.shape[0]
output_size = env.action_space.n
num_episodes = 2000
dis = 0.9
model = tf.keras.Sequential([
tf.keras.layers.Dense(output_size, input_shape = [input_size],
kernel_initializer=tf.keras.initializers.glorot_uniform()) #xavier
])
model.compile(optimizer = tf.keras.optimizers.Adam(learning_rate = learning_rate), loss = 'mse' )
print(model.summary())
with tf.device('/GPU:0'):
rList = []
for i in range(num_episodes):
e = 1./ ((i/10)+1)
rAll = 0
step_count = 0
s = env.reset()
print(s)
done = False
while not done:
step_count += 1
x = np.reshape(s, [1, input_size])
Qs = model.predict(x)
if np.random.rand(1) < e:
a = env.action_space.sample()
else:
a = np.argmax(Qs)
s1, reward, done, _ = env.step(a)
if done:
Qs[0,a] = -100 #'done = 잘못된 행동'이므로 reward로 -100을 줌
else:
x1 = np.reshape(s1, [1, input_size])
Qs1 = model.predict(x1)
Qs[0,a] = reward + dis * np.argmax(Qs1)
model.fit(x = x, y = Qs)
s = s1
print(step_count)
rList.append(step_count)
print("Episodes : {} step : {}".format(i, step_count))
if len(rList)>10 and np.mean(rList[-10:])>500:
break
|
cs |
Cart pole 학습이 안되는 이유 (자세한 건 다음 DQN 강의)
1) network이 너무 작다. (변수 오직 4개)
2) 샘플간 Correlation이 있다.
3) 타겟이 고정되지 않고 움직인다.
'ML&DL > Sung Kim's RL Lecture' 카테고리의 다른 글
| LEC 07. DQN (0) | 2021.01.11 |
|---|---|
| LEC 05. Q-learning on Nondeterministic Worlds! (0) | 2021.01.08 |
| LEC 04. Q-learning (table) (0) | 2021.01.07 |
| LEC 03. Dummy Q-learning (table) (0) | 2021.01.07 |
| LEC 02. Playing OpenAI GYM Games (0) | 2021.01.06 |