목차
Clustering
Clustering이란 라벨이 없는 데이터들을 미리 지정해둔 k개 그룹에 분리하는 작업입니다. 각 그룹으로 묶인 데이터는 유사한 성질을 가져야 합니다. 이때, 유사함을 측정하는 지표로 사용되는 distance measure에 따라 clustering 결과가 달라질 수 있습니다. 이번 포스팅에서는 k-Means와 Mixture of Gaussians Clustering(MoG) Clustering에 다룹니다. 각각의 방법을 이해한 뒤, k-Means가 MoG를 간략히 한 버전임을 이해해봅시다!!
1. k-Means
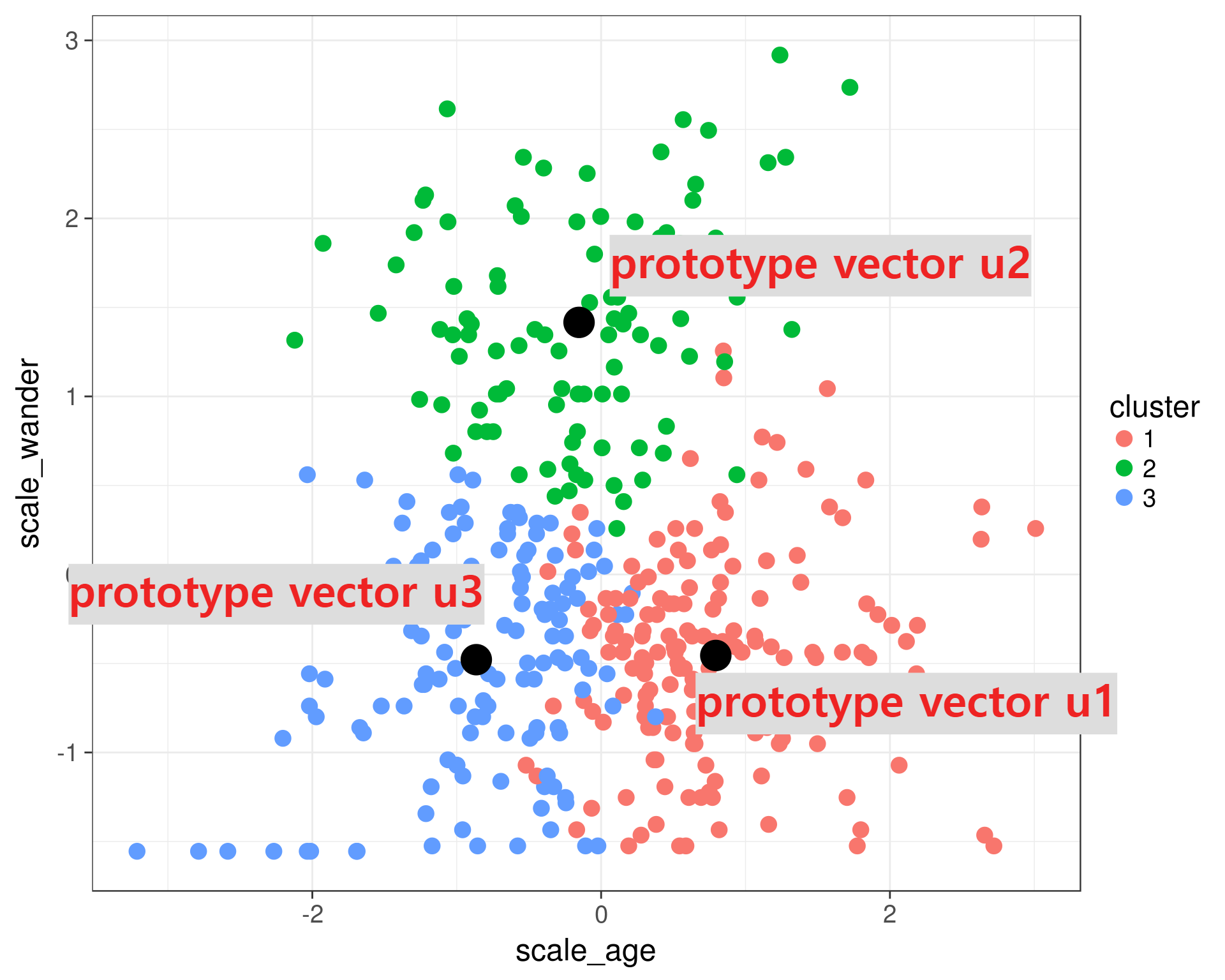
Clustering의 가장 기본적인 알고리즘은 k-Means입니다. 말 그대로, 데이터 셋을 k개의 그룹으로 묶습니다. 각 그룹은 중심 vector (= prototype vector)를 가지며, 각각의 데이터와 그룹을 대표하는 중심 vector간의 Euclidean distance를 계산합니다. 데이터는 중심 vector와의 거리가 가장 가까운 그룹에 속하게 됩니다. 이를 수식으로 나타내면 다음과 같습니다.
데이터를 분리한 k개의 subset $C_j$, 각 그룹에 속한 데이터 수 $N_j$ 에서, 각 중심 prototype vector는 다음과 같이 표현됩니다. $$u_j = \frac{1}{N_j} \sum_{t\in C_j}x_t$$
모든 데이터와 그 데이터가 속한 그룹의 중심 prototype vector간의 거리를 최소하 하는 것이 목적입니다.
$$J = \sum_{j=1}^k\sum_{t\in C_j}|x_t-u_j|^2$$
k-means알고리즘은 2단계로 진행됩니다. 2단계를 더 이상의 변화가 없을 때(수렴)까지 반복합니다.
STEP 1) Assignment step
말 그대로, 데이터를 중심 vector와의 거리가 가장 가까운 그룹에 배정합니다.
STEP 2) Update step
매 assignment step마다 각 그룹에 속한 데이터들이 달라질 것입니다. 따라서 중심 vector를 재설정해야 합니다.
$$u_j^{new} = \frac{1}{N}\sum_{t\in C_j}x_t$$
responsibility $r_{jt}$ 도입
indicator vector의 역할인 responsibilities $r_{jt}$를 도입하여 k-means식을 다시 살펴봅시다. $r_{jt}$는 단순히 데이터 $x_t$가 그룹 j에 속한면 1, 아니면 0을 나타냅니다.
$$\begin{equation}
r_{jt}=\begin{cases}
1, & \text{if $\;\;\arg\min_k |x_t-u_k|^2=j$}.\\
0, & \text{if $\;\;\arg\min_k |x_t-u_k|^2\neq j$}.
\end{cases}
\end{equation}$$
$r_{jt}$를 사용한 k-means 알고리즘은 다음과 같습니다.
STEP 1) Assignment Step : 데이터의 소속인 $r_{jt}$ 계산 (그룹에 속하면 1, otherwise 0)
STEP 2) Update : $u_j$ 업데이트
$$u_j = \frac{\sum_{t=1}^N r_{jt}x_t}{\sum_{t=1}^N r_{jt}}$$
이 경우, 목적함수는 $$J = \sum_{j=1}^k\sum_{t=1}^N r_{jt}|x_t-u_j|^2 \\subject \;to\; R=[r_{jt}] \in \bigg\{ R\in \{0,1\}^{k*N} | \sum_{j=1}^K r_{jt}=1 \bigg\}$$
optimization을 풀어보면, (EM은 4강 후반 및 5강에서 다룹니다.)
STEP 1) Assignment step : $u_{j}$를 고정하고, $r_{jt}$를 조정하여 목적함수를 최적화 합니다. $\rightarrow$ E-step
STEP 2) Update step : $r_{jt}$를 고정하고, $u_j$를 조정하여 목적함수를 최적화 합니다. $\rightarrow$ M-step
Evaluation of Clustering
clustering이 잘 되었는가를 평가하기 위한 2가지 척도, (1) CA (2) NMI 를 소개합니다.
(1) Clustering Accuracy (CA)
ground truth cluster $\tilde c_t$와 예측한 cluster $c_t$가 얼마나 일치하는지 계산합니다.
$$CA = \frac{\sum_{t=1}^N \delta(c_t, \tilde c_t)}{N}$$
$$\begin{equation}
\delta(i,j)=\begin{cases}
1, & \text{if $\;\;i=j$}.\\
0, & \text{otherwise}.
\end{cases}
\end{equation}$$
(2) Normalized Mutual Information (NMI)
우선, mutual information이란 두 개의 분포간의 상호 정보량을 의미하며, 독립일 경우 mutual information은 0 입니다. 이를 측정하기 위해선, joint distribution $p(C_i, \tilde C_j)$과 2개의 marginal distribution의 product인 $p(C_i)p(\tilde C_j)$의 분포가 닮았는지 KL divergence 로 확인합니다. * $p(C_j) = \frac{C_j \text{그룹 에 속한 데이터 수} }{N}$
$$I(C, \tilde C) = KL[ p(C_i, \tilde C_j) || p(C_i)p(\tilde C_j)] =\sum_i\sum_j p(C_i, \tilde C_j) \log_2 \frac{p(C_i, \tilde C_j)}{p(C_i)p(\tilde C_j)} \\= -H(C_i, \tilde C_j) + H(C_i) + H(\tilde C_j)$$
$C_i$와 $\tilde C_j$가 독립이라면, $p(C_i, \tilde C_j) = p(C_i)p(\tilde C_j)$ 이고, $\log_2 \frac{p(C_i, \tilde C_j)}{p(C_i)p(\tilde C_j)}= \log_2 1 =0$이 되어 mutual information이 0이 됩니다. 반면, dependent할 수록 mutual information값은 커집니다.
Mutual Information : $$I(X,Y) = H(X) + H(Y) -H(X,Y) \\= H(X) -H(Y|X) = H(Y)-H(X|Y) \\= H(X,Y) - H(X|Y) - H(Y|X)$$
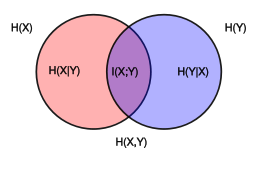
Normalized mutual information(NMI)를 사용하는 이유는 서로 다른 random variable을 갖는 $X, Y$를 비교할 때, normalize를 수행합니다.
$$NMI(C, \tilde C) = \frac{I(C, \tilde C)}{[H(C)+ H(\tilde C)]/2}$$
Soft k-means
Soft k-means 는 '하나의 데이터는 하나의 집합에만 속한다'라는 k-mean의 제약 조건을 완화시킨 버전입니다. 따라서 데이터 $x_t$가 그룹 j에 속할 가능성을 responsibility $r_{jt}$에 반영해야 합니다. softmax와 같이 계산하며 $r_jt$는 그룹 j에 속할 확률을 의미합니다.
Assignment Step:
$$r_{jt} = \frac{exp \{ -\beta |x_t-u_j|^2 \} }{ \sum_l exp \{ -\beta |x_t-u_l|^2 \}}, \;\;\; \sum_j r_{jt}=1$$
Update Step:
$$u_j =\frac{\sum_{t=1}^N r_{jt}x_t}{\sum_{t=1}^N r_{jt}}$$
Objective function :
$$J_{SK} = \sum_{t=1}^N\sum_{j=1}^K r_{jt}|x_t-u_j|^2 - \frac{1}{\beta}\sum_{t=1}^N\sum_{j=1}^K r_{jt}\log\frac{1}{r_{jt}}$$
2. Mixture of Gaussians (GMM, Gaussian mixture model)
다음 클러스팅 방법은 MoG입니다. MoG는 mixture model에 해당합니다. 말 그대로, 여러 모델을 조합하여 사용하는 방법론입니다. 여러 모델을 사용한다는 점에서 semi-parametric model에 해당합니다.
MoG, Mixture of Gaussians(= GMM, Gaussian mixture model)는 데이터셋이 여러 가우시안 모델의 조합으로 생성되었다고 가정하며, MoG Clustering이란 각 데이터가 'k개의 가우시안 모델 중 어떤 가우시안 모델에 속하는가'로 데이터셋을 분류하는 방법입니다.
다음 그림은 데이터셋을 3개의 가우시안 모델로 분류한 MoG입니다.
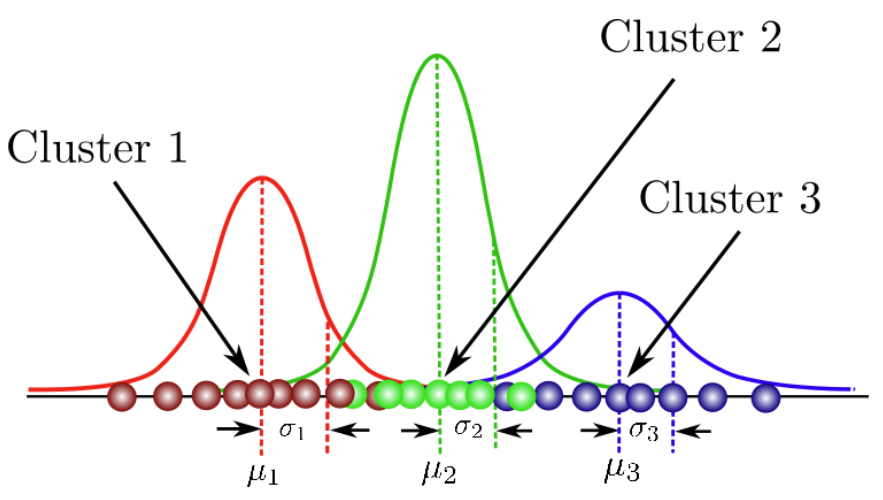
그럼 MoG에서 우리가 구해야 할 parameter는 무엇일까요??
우선 각각의 가우시안 모델의 개형을 알아야 하니, (1) 평균($u_j$) 와 (2) 분산(univariate : $\sigma_j$, multivariate : $\Sigma_j$)를 찾아야 합니다. 또한 (3) 데이터가 특정 모델일 확률 ($\pi_j$)를 알아야 합니다. $\color{green} p(w_j)$는 mixing parameter로 불리며 특정 가우시안 모델에 속할 prior probability입니다. parameter값을 모두 구하게 되면, 데이터의 확률을 계산할 수 있게 됩니다. 모델 j에 속할 확률 $\color{green}p(w_j)$과 모델 j일 때의 데이터 확률 $\color{red}p(x|w_j)$을 모든 group($j = 1,\cdots,k)$에 대해 marginal하여 구하면 됩니다.
Mixture distribution :
$$p(x) = \sum_{j=1}^k p(x, w_j) = \sum_{j=1}^k \color{red}p(x|w_j) \color{green}p(w_j)$$
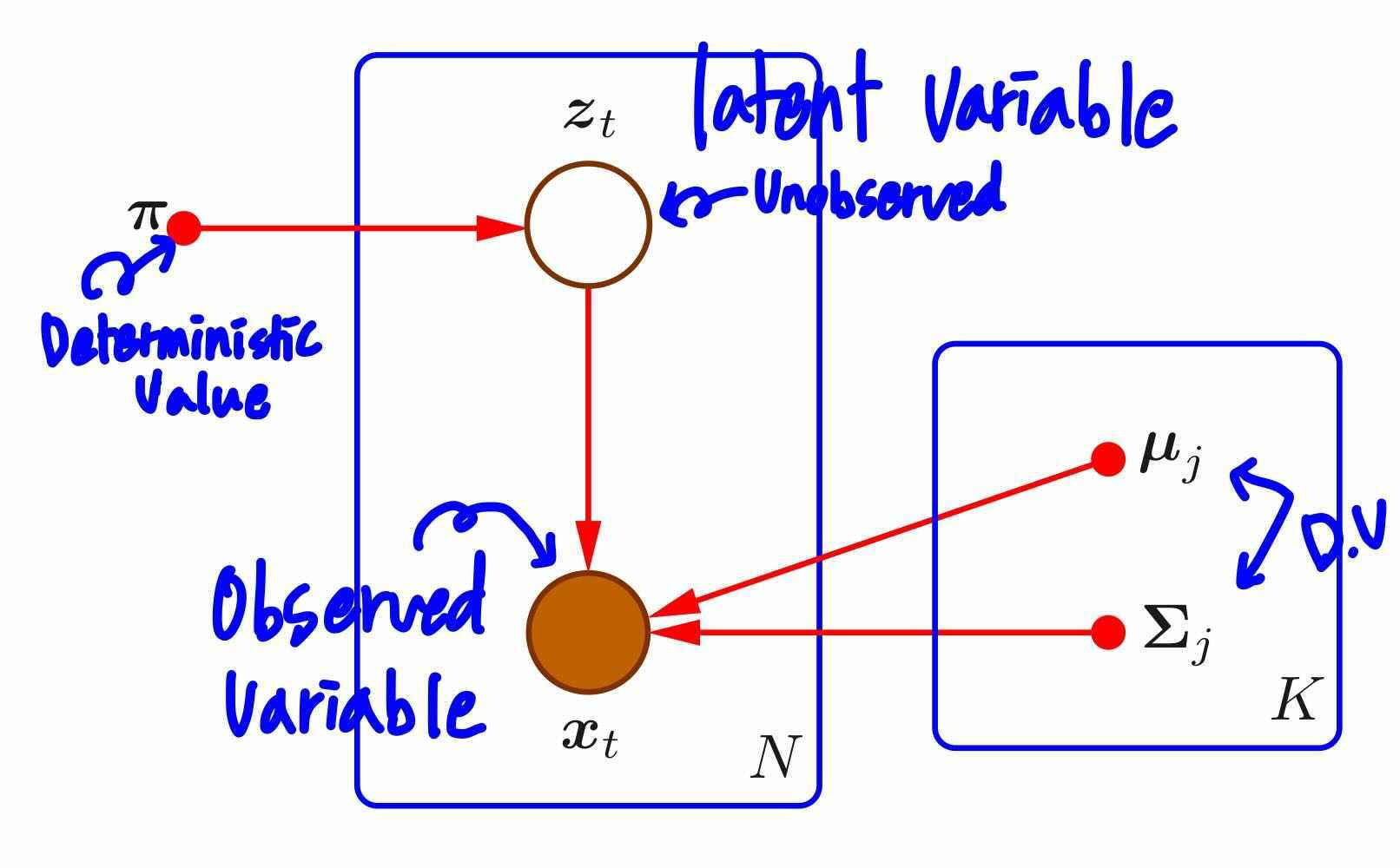
같은 내용을 graphical model로 살펴봅시다. 우선, 데이터가 k개의 가우시안 모델, 그 parameter $u_j, \Sigma_j$ 에 의해 생성되었다는 것을 확인할 수 있습니다. 그럼 상단의 $z_t$는 무엇일까요? 바로 앞선 설명에서 데이터가 모델에 속할 확률인 $\pi$를 parameter로 갖는 변수입니다. 이때, $z$는 latent variable(잠재변수)에 해당합니다. 위키백과의 설명에 따르면, 잠재 변수는 구성개념이 직접적으로 관찰되거나 측정이 되지 않는 변수를 의미합니다. 우리의 데이터 $x$는 관찰된 대상이지만, 각각의 데이터가 어떤 모델에 속해있는지 latent variable $z$는 모릅니다. MoG에서는 latent variable을 사용하므로써, 자연스럽게 여러 모델이 존재할 경우 데이터의 확률을 표현할 수 있습니다.
$z_t = [0,\cdots,1,\cdots,0]^T$ 로 데이터 t가 속한 모델 j의 index에 1, 나머지는 0으로 binary value로 표현합니다. 그럼 $p(z_t) =\prod_{j=1}^K \pi_j^{z_{jt}}$ 로 나타낼 수 있고, $z_t$를 안다면(즉, 데이터가 속한 모델을 안다면), 데이터의 확률도 다음과 같이 표현할 수 있게 됩니다. $$p(x_t|z_t) = \prod_{j=1}^K N(u_j, \Sigma_j)^{z_{jt}}$$
어떤 parameter를 최적화 할 지 알았는데, 그 방법은 무엇일까요?? MoG의 performance measure는 log likelihood function입니다. 데이터셋의 확률을 가장 최대로 하는 parameter, $\{\pi_j , \u_j, \sigma_j\}$를 찾아야 합니다.
우선적으로, Complete data($x$와 $z$)의 complete data log likelihood, &L_c&를 계산하면 다음과 같습니다. 이때 혼동하면 안되는 것은, 우리가 실제로 최대화 해야할 값은 complete data의 log likelihood 가 아닌 그냥 data log likelihood $L = \sum_{t=1}^N log p(x_t)$입니다. 하지만 marginal distribution $p(x)$을 optimize하는게 어려우니, 대신 latent variable 을 사용하여 그 variable과 latent variable간의 joint distribution $p(x,z) = \sum_{j=1}^k \color{red}p(x|w_j) \color{green}p(w_j)$을 다루고 있는 것 입니다. 이것이 latent variable의 진가입니다!!
* data log likelihood 가 아닌 complete data log likelihood를 optimize하는 parameter를 찾아도 되는 이유는 다음 포스팅 <5. EM>에서 다루겠습니다 :)
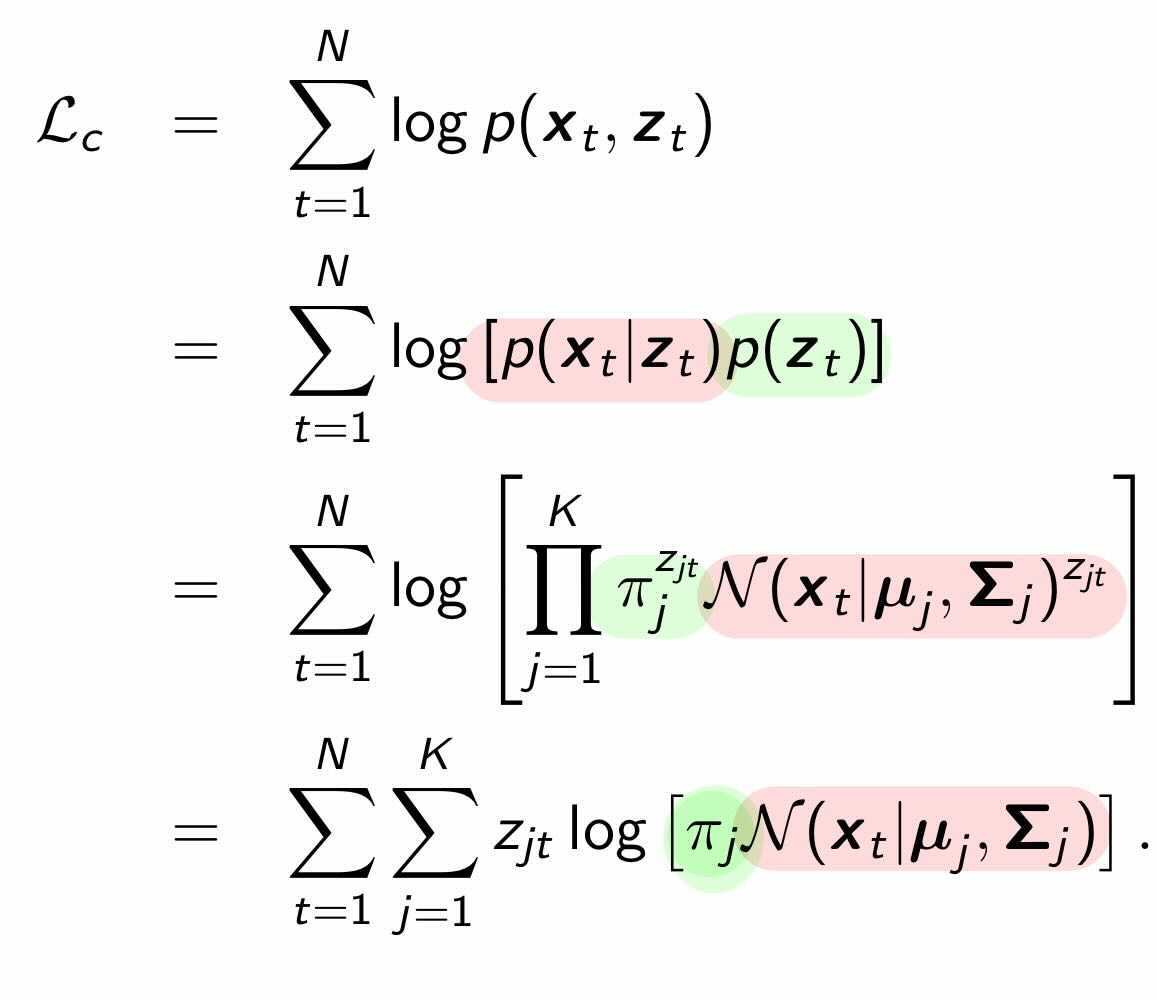
자, 근데 한가지 문제점이 더 있습니다. 우리는 latent variable $z$를 모릅니다. $z$는 이름 그대로 관찰되지 않은 변수죠!! 이럴 경우, 우리는 Expectation Maximization(EM)알고리즘을 사용합니다. 바로, latent variable의 기댓값, expectation을 사용하자는 것입니다. $$z_{jt} \leftarrow p(w_j|x_t)$$ latent variable $z_{jt}$에 대한 expectation을 posterior distribution $p(w_j|x_t)$로 사용하는 이유도 다음 포스팅 <5. EM>에서 다룹니다 :)
Expected complete data loglikelihood를 구하는 단계가 EM의 E step에 해당합니다.
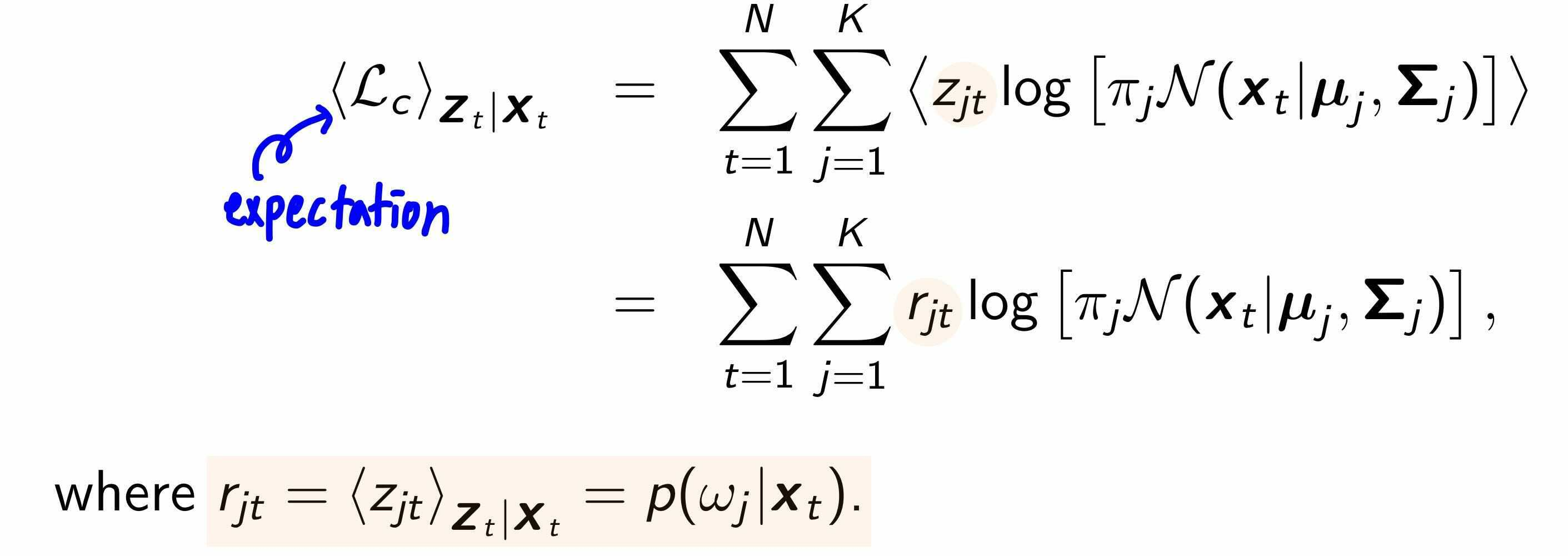
다음으로, EM의 M step을 수행해야합니다.
expected complete data log likelihood를 최대화 할 parameter $\{u_j, \Sigma_j, \pi_j\}$를 찾습니다.
마지막 $\pi_j$ 를 구할 때는, $\sum_j^k \pi_j = 1$이라는 제약 조건이 있으므로, Lagrange를 사용합니다.

단순 MoG이외에도 Bayesian MoG, Infinite Misture of Gaussians 모델도 존재합니다.
Bayesian MoG는 parameter $\{u_j, \Sigma_j, \pi_j\}$를 random variable로 가정합니다. 이때 conjugate prior를 사용하여 multinomial인 $\pi$에는 Dirichlet distribution을, multivariate gaussian인 $u_j, \Sigma$를 위해선 Normal-Wishart distribution을 사용합니다.
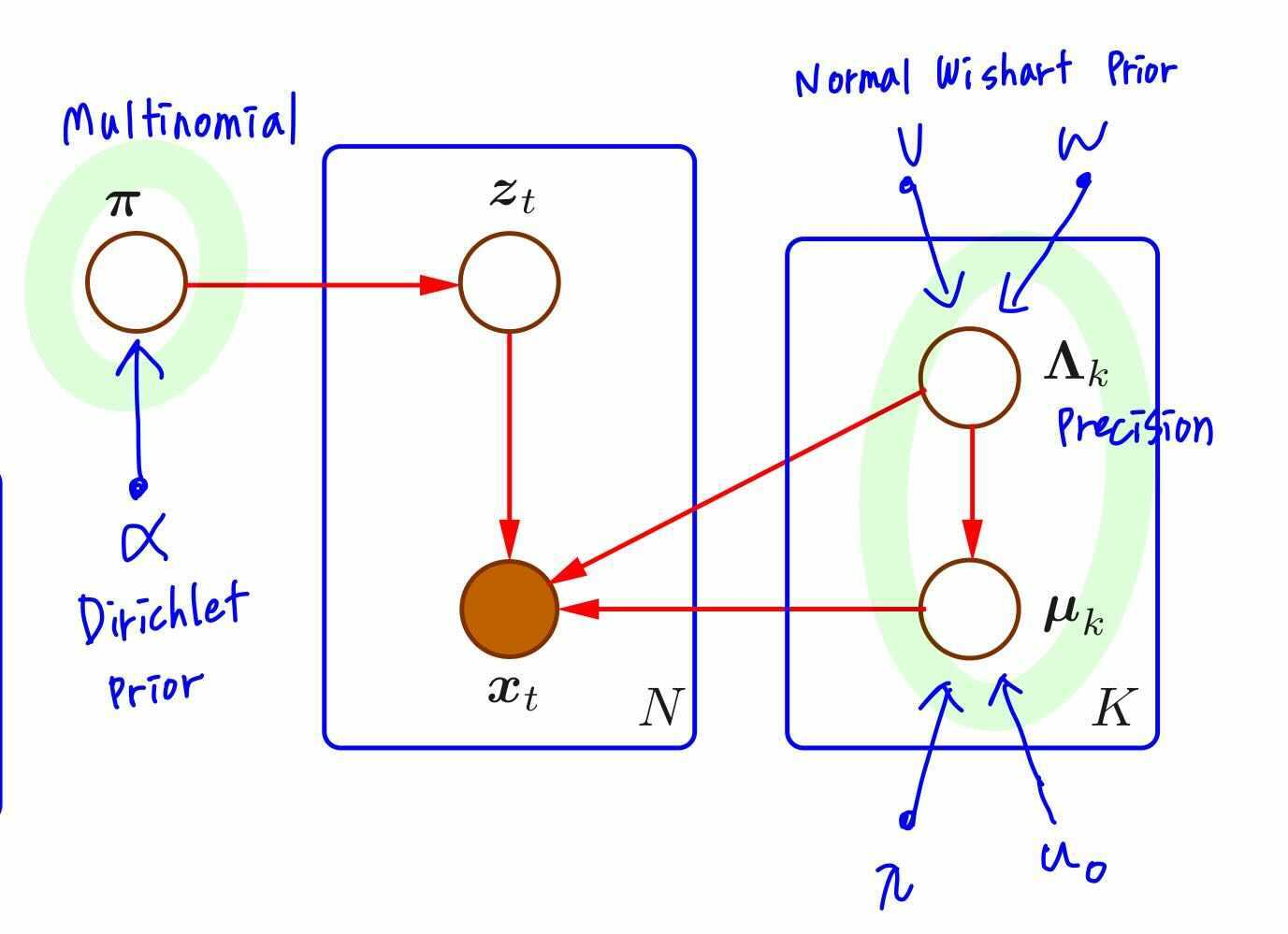
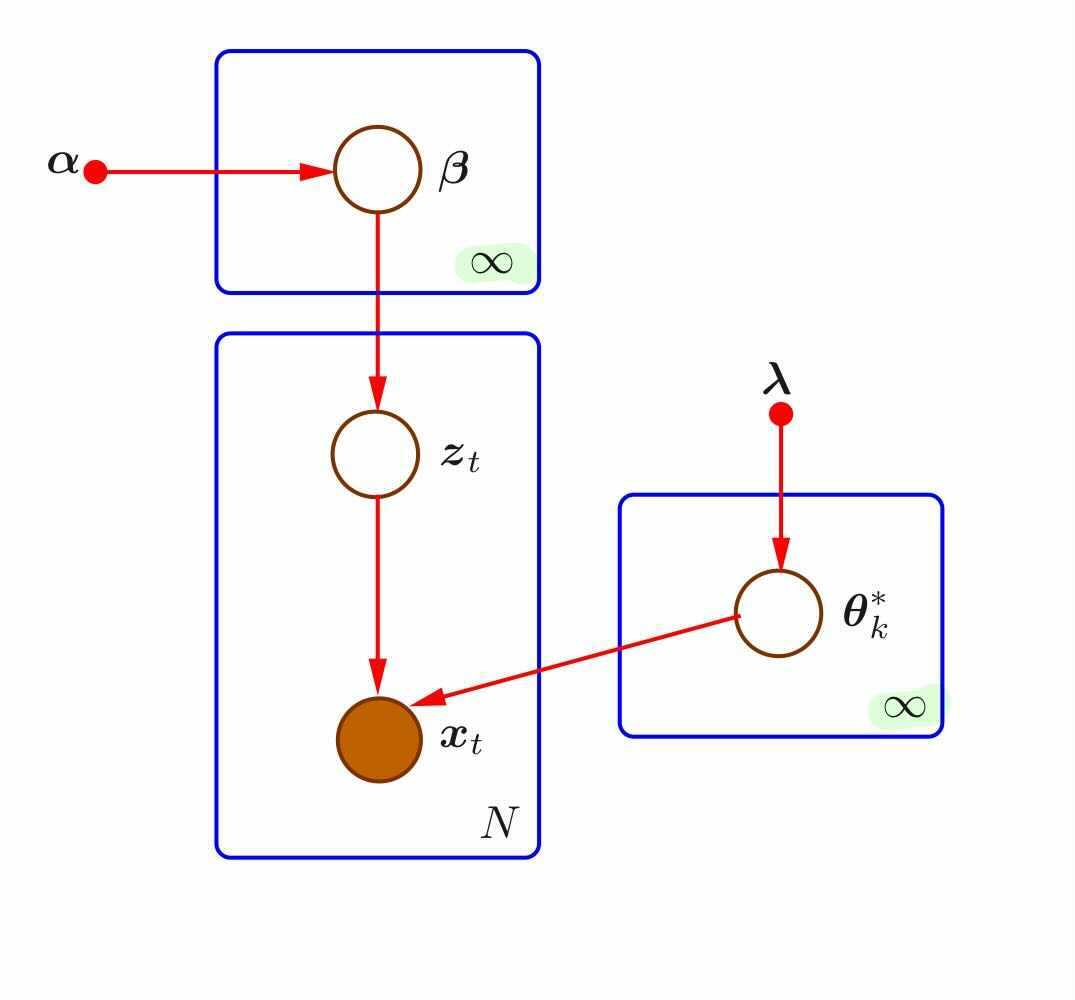
3. k-Means & MoG
포스팅 도입에 k-Means가 MoG를 간략히 한 버전이라고 설명했습니다. 두개의 가정이 있으면 MoG가 k-Means로 바뀐답니다. 첫번째 가정은 모든 가우시안 모델이 동일한 확률을 가진다는 것입니다. $\pi_j = \frac{1}{k} , j = 1, \cdots, K$
두번째 가정은 $\Sigma$를 isotropic distribution으로 가정하고, $\sigma^2 \rightarrow 0$ 입니다.
그러면 responsibility 가 k-Mean과 같이 discrete해집니다!!
(증명은 아래 링크를 참고해주세요)
- E step
$$r_{jt} = p(w_j|x_t) = \begin{cases} 1 & \text{if nearest group j} \\ 0 & otherwise \end{cases}$$
- M step
$$u_j^{new} = \frac{1}{N}\sum_{t\in S_j}x_t$$
'ML&DL > Pattern Recognition and Machine Learning' 카테고리의 다른 글
| 6. Latent Variable Models PCA & FA & MFA (0) | 2022.11.04 |
|---|---|
| 5. Expectation Maximization(EM) (1) | 2022.10.25 |
| 3. Density Estimation (0) | 2022.09.20 |