목차
EM Algorithm
이번 포스팅에서는 Expectation maximization, EM알고리즘을 자세히 알아보도록 합시다. 이전 포스팅에서 latent variable이 있는 MoG를 EM알고리즘으로 풀었고, 2개의 의문을 남겼습니다.
(1) 왜 complete data log likelihood를 사용하는지.
(2) E-step에서 왜 posterior distribution을 사용하는지.
이번 포스팅에서 샅샅이 밝혀보도록 하겠습니다!!
1. Mathematical preliminaries
우선, EM 알고리즘을 이해하기 위해 필요한 선수 지식을 소개합니다.
(1) Jensen's Inequality, (2) Information theory, (3) Gibb's Inequality를 살펴보도록 합시다.
(1) Jensen's Inequality

Jensen's Inequality는 convex function $f(x)$의 성질을 일반화 한 이론입니다. 우선 convex function은 $\color{red}f(tx_1 +(1-t)x_t \color{black}\leq \color{blue}tf(x_1) + (1-t)f(x_2)$ 성질을 만족하는 함수입니다. 두 점 사이의 내적점에서의 함수값이 그 두 점의 함수값의 평균보다 작습니다!! 따라서 convex function은 그림과 같이 오목한 개형을 가집니다.
Jensen's Inequality는 convex function이고, x가 random vector의 경우, $$\color{red}f(E\{x\}) \color{black}\leq \color{blue}E\{f(x)\}$$ (*concave function일 경우, 부등호 방향이 바뀝니다.)
[증명]
$\color{red}f(\sum_{i=1}^N p_i x_i) \color{black}\leq \color{blue}\sum_{i=1}^N p_i f(x_i)$
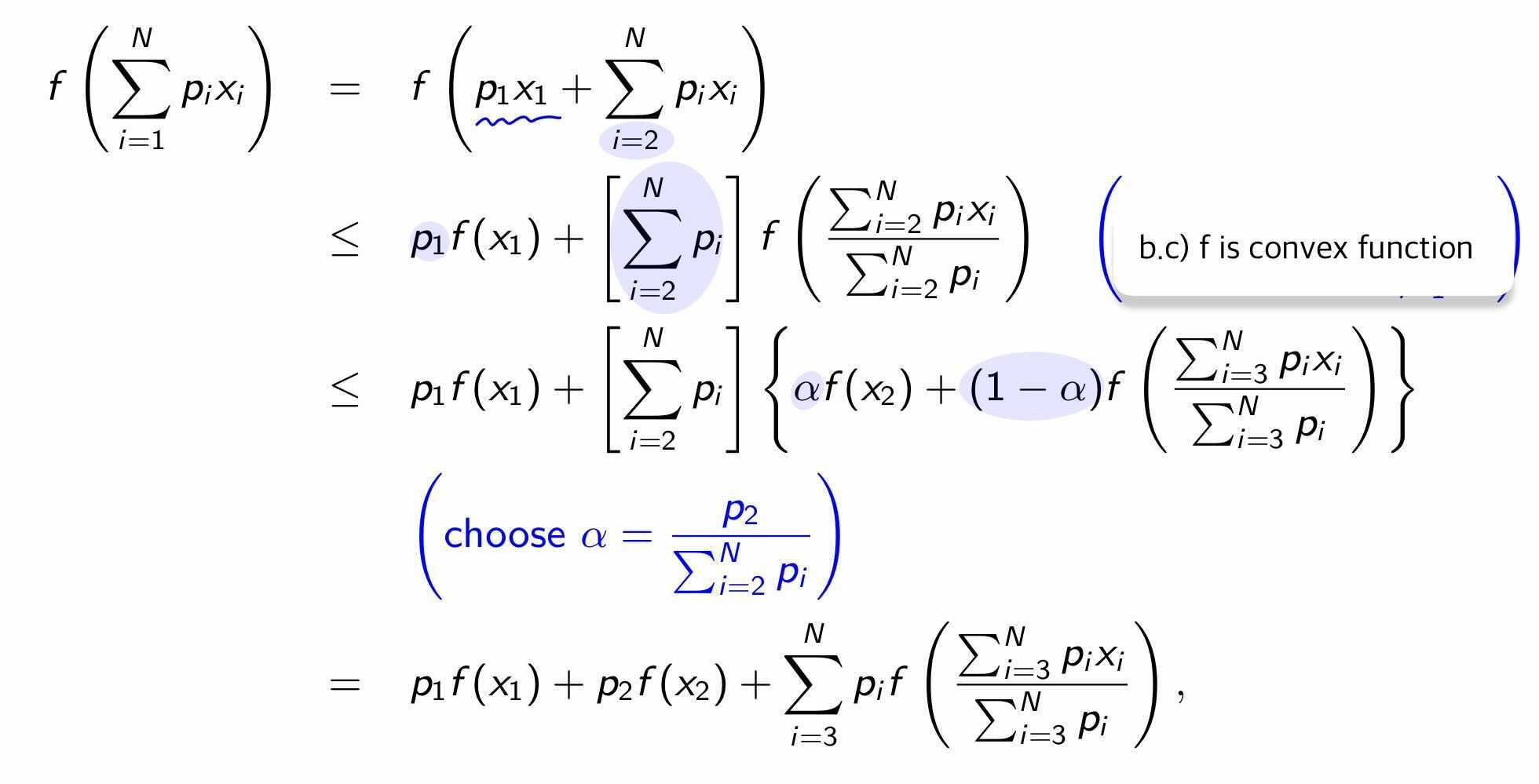
(2) Information theory
Information | Entropy | Relative entropy | Mutual information
Information은 놀람의 정도라고 해석할 수 있습니다. 발생할 가능성이 적은 사건일 수록, 놀랍고 많은 정보를 포함한다고 봅니다. (해가 서쪽에서 뜨겠네.. 별 놀랄일이 다있네) 그래서 information 의 수식은 발생 가능성에 반비례하게 측정합니다.
$$\text{Information} = \log \frac{1}{p(i)} = -\log p(i)$$
Entropy는 평균 정보(average information)의 양입니다.
$$H = \sum_{i=1}^N p(i)\log \frac{1}{p(i)}$$
Relative entropy는 KL divergence(Kullback-Leibler)입니다. 2개의 distribution이 닮아있는지 entropy비교를 통해 측정합니다. KL은 assymetric 함수입니다. $KL[p|q] \neq KL[q|p]$ 달라요!!
$$KL[p|q] = \sum_{x\in X} p(x)\log \frac{p(x)}{q(x)}$$
$$= \sum_{x \in X}p(x) \log \frac{1}{q(x)} - \sum_{x \in X} p(x) \log \frac{1}{p(x)}$$
Mutual information는 상호 정보량을 의미하며, joint distribution과 marginal distribution의 곱 간의 relative entropy입니다. 독립일 경우 mutual information은 0 입니다. 이전 포스팅에서 k-means의 평가 척도로 소개한 적이 있습니다. ground truth cluster $\tilde c_t$와 예측한 cluster $c_t$가 얼마나 일치하는지 계산하기 위해 mutual information을 사용했습니다.
$$I(C, \tilde C) = KL[ p(C_i, \tilde C_j) || p(C_i)p(\tilde C_j)] =\sum_i\sum_j p(C_i, \tilde C_j) \log_2 \frac{p(C_i, \tilde C_j)}{p(C_i)p(\tilde C_j)} \\= -H(C_i, \tilde C_j) + H(C_i) + H(\tilde C_j)$$

(3) Gibb's Inequality
KL divergence 가 항상 0보다 크거나 같으며, p=q일때 0이라는 이론입니다. KL은 두 분포의 차이를 측정하는 데, 같은 분포 ($p=q$)라면 차이는 당연히 0일 것입니다.
$$KL[p|q]\geq 0 \text{with equality iff } p=q$$
[증명]

KL이 최소값일 때를 Lagrangian을 사용해서 확인해봅시다.
$$L = KL[p|q] + \lambda(1-\sum_i p_i)=\sum_i p_i \log \frac{p_i}{q_i}+\lambda(1-\sum_i p_i)$$
다음 식을 편미분 하면, $\frac{\partial L}{\partial p_k} = \log p_k - log q_k + 1- \lambda = 0$이 됩니다.
여기서, $p_k = q_k e^{\lambda-1}$ 이고, $\sum_i p_i =1$를 만족하려면 $\lambda = 1, p_i = q_i$ 가 됩니다.
Hessian을 구해보면 $\frac{\partial^2 L}{\partial p_i^2} = \frac{1}{p_i}$, $\frac{\partial^2 L}{\partial p_i \partial p_j} = 0$이기에 positive definite이고, 이는 strictly covex에 해당합니다.
따라서 $p_i=q_i$가 unique global optimum임을 확인할 수 있습니다.
자, 이제 EM 을 다룰 준비를 마쳤습니다!!

2. EM Algorithm
Expectation Maximization 알고리즘은 Maximum likelihood parameter을 찾는데 사용됩니다. 이전 포스팅에서 MoG의 performance measure는 log likelihood function 이었고, 이를 최대화하기 위한 parameter를 EM을 사용하여 찾았습니다. Expectation step과 Maximization step으로 구성되어있고 두 단계를 반복하며 최적의 paramter를 찾습니다.
Expectation step에서는, 현재 구한 parameter와 주어진 데이터셋으로 missing 혹은 unobserved data를 예측합니다.(MoG에서의 latent variable) Maximization step에서는, complete data(데이터 셋 + 앞서 예측한 unobserved data)를 사용하여 최적의 parameter를 찾습니다.
Lower bound of EM
관찰된 variable을 $x$ (eg. 데이터셋), 관찰되지 않은 variable을 $s$, model parameter를 $\theta$ 라고 합시다.
구해야할 것은 log-likelihood : $L(\theta) = \log p(x|\theta) = log \int p(x,s|\theta) ds$
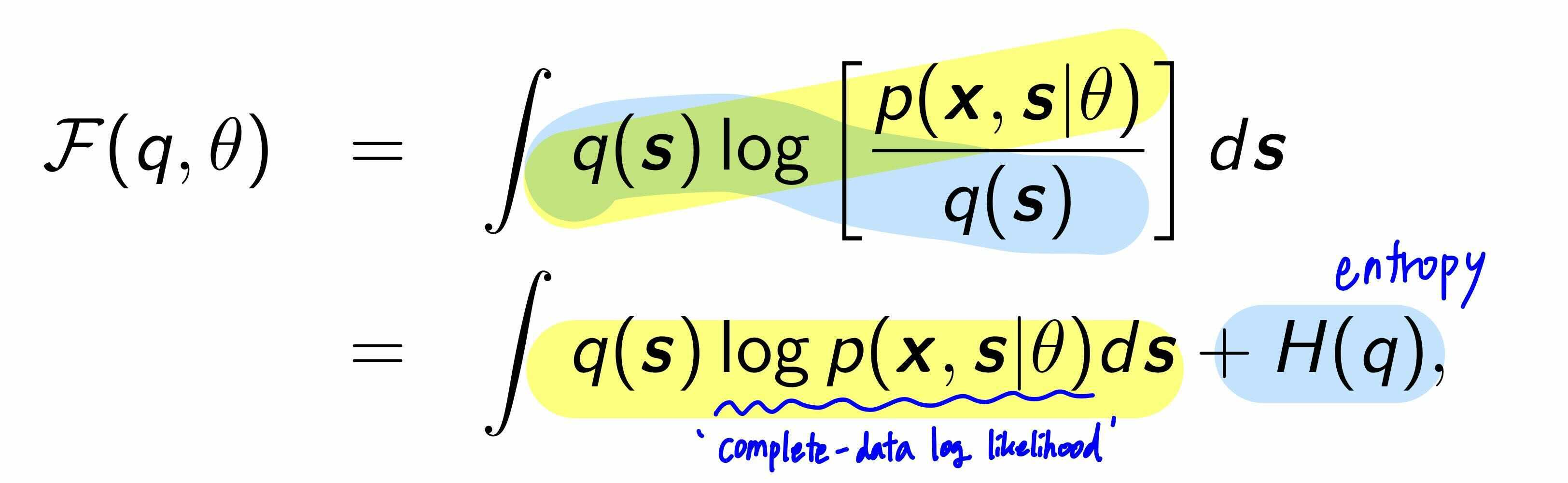
이때 Jensen's inequality를 사용하면 log-likelihood 의 lower bound $F(q,\theta)$를 구할 수 있습니다. $\log$ 는 concave function이고, $q(s)$는 unobserved variable의 distribution입니다.

우리는 Maximum likelihood parameter을 찾고 싶습니다. 하지만, data log-likelihood $\log p(x| \theta)$ 를 구하기 어렵습니다. 그래서 아쉬운대로 EM알고리즘에서는 lower bound $F(q,\theta)$를 optmize하려고 합니다. Jensen's inequality에 의해서, $F(q, \theta)$를 업데이트 하는 것은 절대로 log likelihood 를 줄이지 않습니다.($F(q,\theta)$ 는 log likelihood의 'Auxiliary funciton' !!) 그래서, lower bound를 분석해보았더니, 마침 complete-data (observed+ unobserved variable) log- likelihood을 포함하고 있습니다. complete data log likelihood는 구하기 쉬우니 너무너무 잘된 일입니다 :)
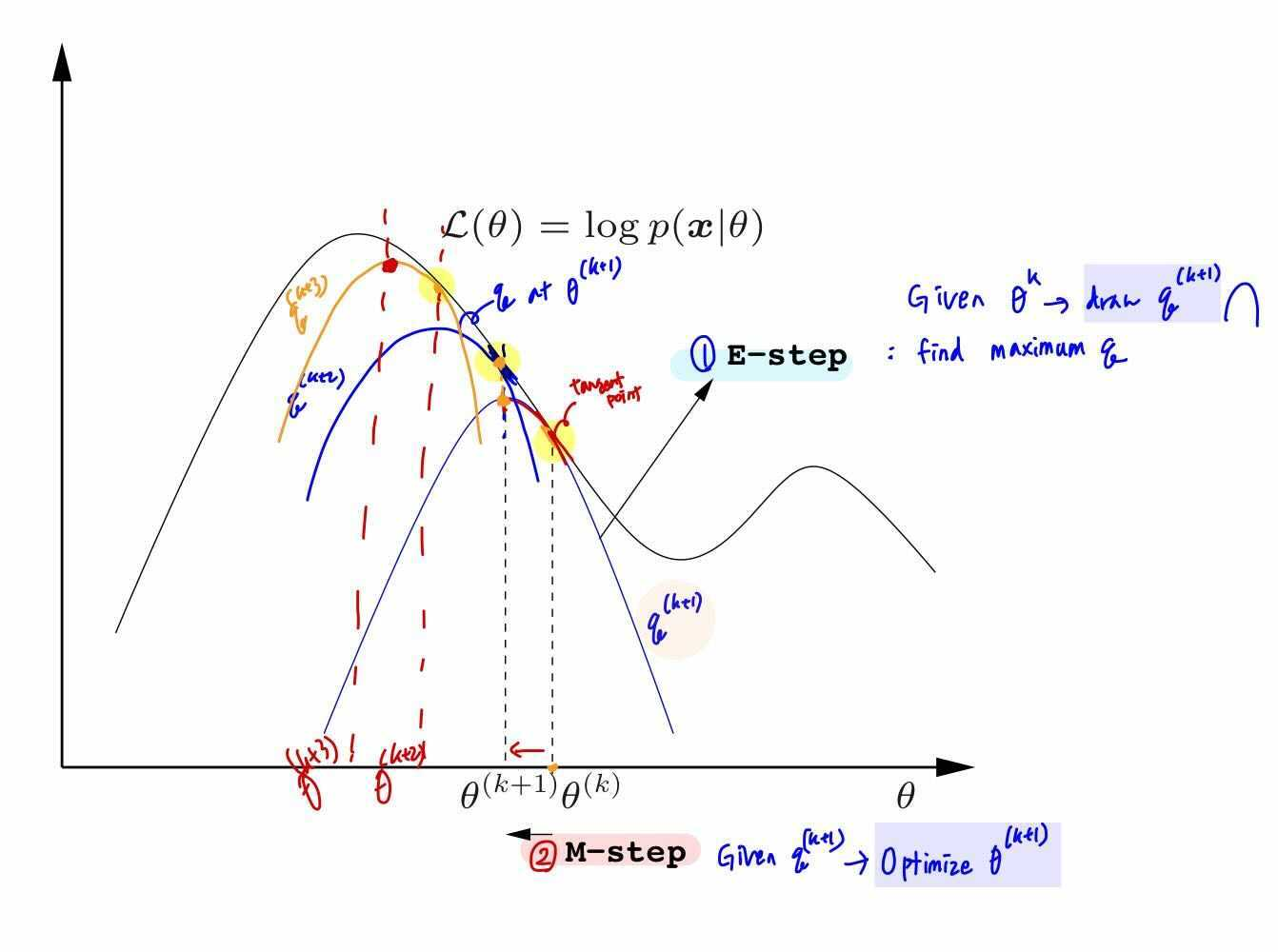
Graphical Illustration of EM
EM 알고리즘에서 Estep에서는 현재의 parameter $\theta^k$의 상황에서 $q^{k+1}$를 update합니다.
M step에서는 새롭게 업데이트 된 $q^{k+1}$를 바탕으로 paramter를 $\theta^{k+1}$로 최적화 합니다.
이 과정을 반복하면서 최적의 parameter를 찾습니다.
Difference between log-likelihood & lower bound
log-likelihood $L(\theta)$ 와 lower bound $F(q,\theta)$의 차이를 구하여, E step에서 $q$를 어떤 값으로 업데이트 해야하는지 알아봅시다!!
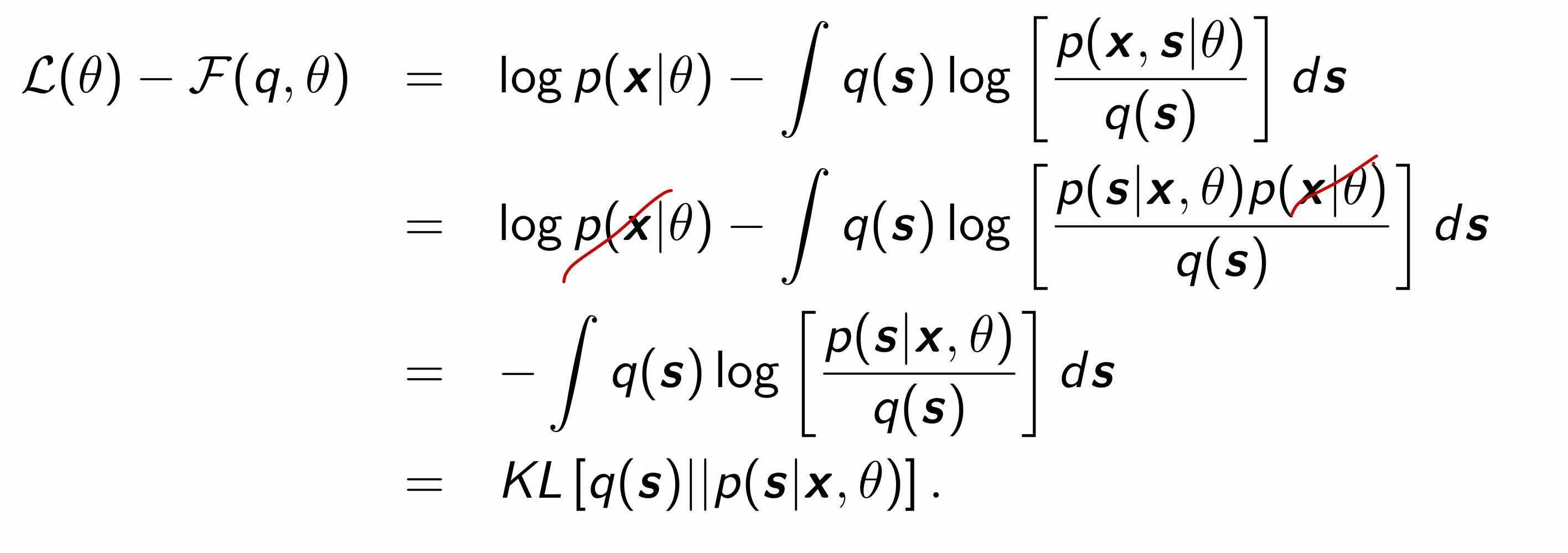
$L(\theta) - F(q, \theta) = KL[q(s) | p(s|x, \theta)]$ 가 됩니다.
Gibb's inequality에 따라 항상 KL은 0보다 크거나 같으며, $q(s) = p(s|x,\theta)$일 경우, $KL[q(s)|p(s|x,\theta)]=0$ 입니다. 따라서 현재의 parameter의 상황에서 lower bound를 최대화 하기 위해선, $q(s) \leftarrow \text{posterior distribution : }p(s|x,\theta)$으로 업데이트 해야합니다.


* 앞서 설명한 EM의 정석 이외에도, 여러 버전이 존재합니다.
Incremental EM의 경우, Partial E-steps을 수행하는 EM알고리즘으로 unobserved variables가 보통 independent하기 때문에 간단한 variable부터 업데이트 합니다. Generalized EM의 경우, Partial M-steps에 해당하며 M step에서 최대의 parameter을 찾는 대신, 기존의 parameter를 개선시키기만 하는 전략입니다.
'ML&DL > Pattern Recognition and Machine Learning' 카테고리의 다른 글
| 6. Latent Variable Models PCA & FA & MFA (0) | 2022.11.04 |
|---|---|
| 4. Clustering (1) | 2022.09.22 |
| 3. Density Estimation (0) | 2022.09.20 |