목차
Latent Variable Model
이번 포스팅에서는 Expectation maximization, EM알고리즘을 자세히 알아보도록 합시다.
1. Latent Variable Model
ff
2. Principal Component Analysis (PCA)
PCA는 데이터의 dimension을 줄이기 위한 대표적인 방법입니다.
원래의 데이터셋의 특징은 잘 살리면서도, 차원을 줄이기 위해선 어떻게 해야할까요? 원래의 데이터를 새로운, 더 작은 차원의 projected space에 투영 시켰을 때, 데이터셋의 분산을 가장 크게 하는 orthogonal projection을 찾는 것이 핵심 아이디어입니다. '분산을 크게 한다'의 직관적인 의미는 '데이터를 잘 퍼트린다'와 같습니다. 즉, 차원 축소 후에도 데이터끼리 잘 구분되며. 데이터의 특징들이 뭉개지지 않게 차원을 줄이고자 하는 PCA는 좋은 차원 축소 방법이라고 판단할 수 있습니다.
이제 구체적인 방법을 수식적으로 살펴봅시다. 데이터 $x$를 $W$ projection을 통해 $D \rightarrow d$로 차원을 줄입니다.
$$y = W^Tx, \;\; \text{where}\; y \in R^D, x \in R^d (d < D), W^TW=I $$
데이터셋 $X$의 분산을 가장 크게 하는 $W$는 어떻게 찾을 수 있을까요?
여러 방법이 있지만, 그 중 Eigen Value Decomposition(EVD)을 소개합니다.
PCA using EVD
Step1) Data centering : data를 mean centering합니다.
Step2) 데이터의 covariance matrix $C= XX^T \in R^(DxD)$에 대해서 EVD를 통해 rank-d approximation을 찾습니다.
$$C \approx U\Sigma U^T$$
$$X \in R^{D*N}, \; U \in R^{D*d}, \; \Sigma $$
$w_i$($W$의 i번째 column)가 데이터의 covariance matrix의 i번째로 큰 eigen value의 eigen vector와 일치합니다.
Step3) 변환 결과인 Principal component score Y를 계산합니다.
$$Y=U^TX$$
증명은 Lagrance Multiplier를 통해 가능합니다.
- 변환 결과인 $y$의 분산 : $y = w^Txx^Tw$
- 제약 조건 : $w^Tw=1$
$$J = w^Txx^Tw - \lambda(w^Tw-1)$$
$$\frac{\partial J}{\partial w} = 2xx^Tw-2\lambda w = 0$$
$$xx^Tw = \lambda w$$
따라서 eigen vector의 정의에 의해, $w$가 covariance matrix $xx^T$의 eigen vector일 때 최대가 됩니다.
* covariane matrix 의 특징
1) Symmetric : eigen vector are orthogonal
2) Semi-positive definite : eigen values must be $\geq 0$
3. Factor Analysis
Factor Analysis도 PCA와 같이 차원 축소에 사용되는 방법입니다.
FA의 핵심 아이디어는 observed variable(indicator, 국어, 영어, 수학 점수 etc.) 의 내막에는 factor(수리 능력, 언어능력)이 존재한다는 것입니다. observed variable이 더 적은 차원의 factor들로 표현되기 때문에 차원을 축소할 수 있습니다. 추가적으로, 각각의 variable이 unique error(국어, 영어, 수학 능력 etc.)를 가진다고 가정합니다. 따라서 observed variable은 factor의 linear combination뿐만 아니라 unique error의 합으로 구합니다.
국어 점수 = $\alpha$x수리능력 + $\beta$x언어능력 + 국어능력
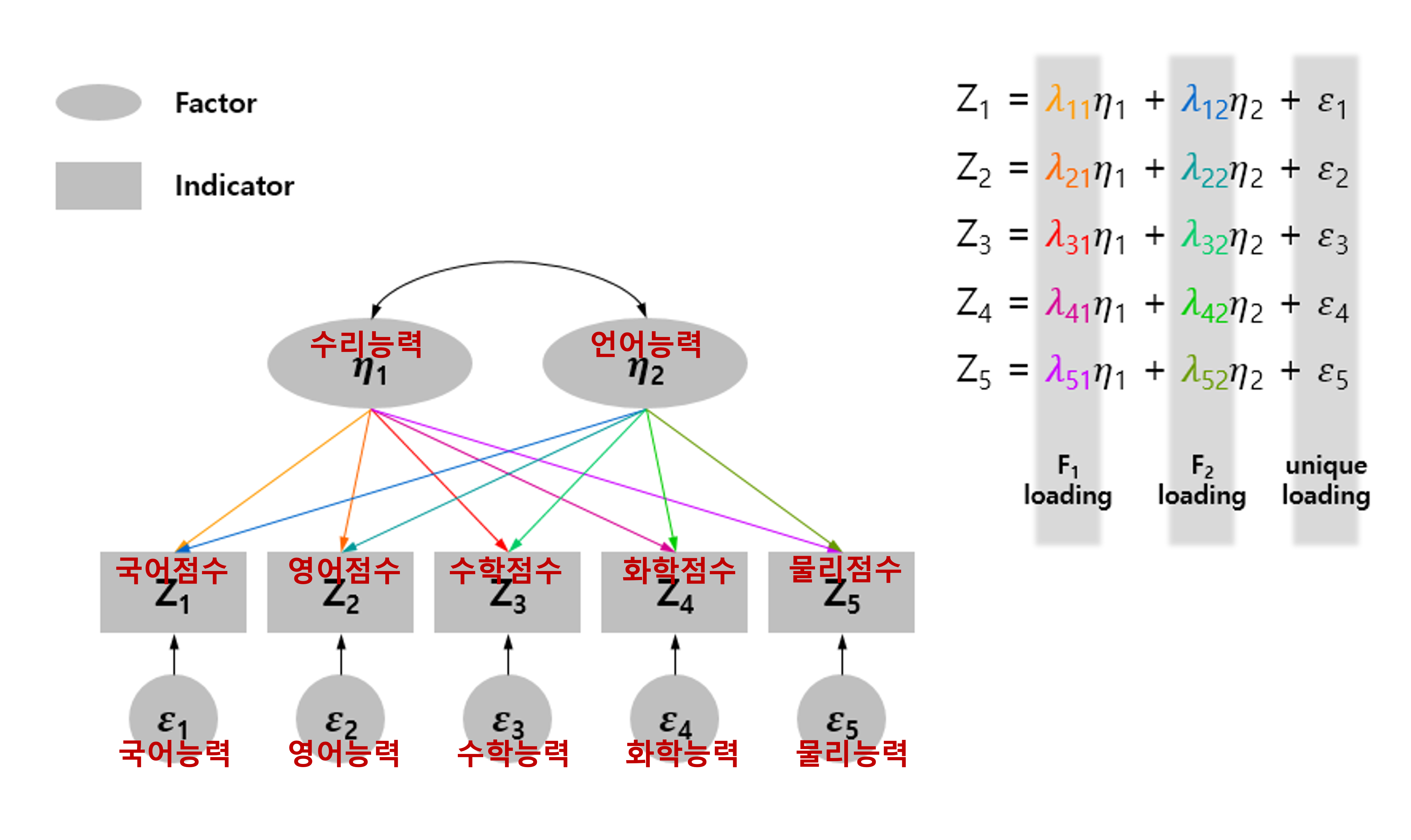
FA 수식
FA에 대한 감을 잡았으니, Graphical Model과 함께 수식적으로 분석해봅시다.
Graphical Model의 기호 표현에 따라,
$$x = As+\epsilon , \;\;s \sim N(0,I), error \sim N(0,\Sigma) \Sigma \;\text{: diagonal matrix}$$
$s$는 $d$차원의 Gaussian latent variable입니다. ($d<<D$, $D$ : 데이터 x의 차원)
$$p(s_t)= N(s_t|0,I)$$
latent variable이 주어졌을 때, observed variable x가 independent해지며, distribution의 다음과 같습니다.
$$p(x_t|s_t) = N(x_t|As_t, \Sigma)$$
Marginal은 다음과 같이 계산됩니다.
$$p(x) = N(0, AA^T+\Sigma)$$
따라서 FA의 목적은, x의 covariance structure을 잘 표현할 수 있는 $A, \Sigma$를 찾는 것 입니다.
d개의 factor는 마치 PCA의 principal component와 같은 역할을 합니다.
columns of A span the space of the first d princial components
isotropic Gaussian noise : ML FA -> probablistic PCA
zero noise : ML FA -> EM-PCA

PCA vs FA
여기서 잠깐, PCA와 다른 점 3가지를 살펴봅시다. -> direction, error $\Sigma$, latent variable $s$사용.
1) direction
PCA의 경우, $y=W^Tx$로 observed variable $x$의 linear combination조합으로 새로운 variable $y$를 만듭니다.
하지만, FA의 경우, $x = As + \epsilon$ 로 unobserved variable인 factor $s$로 observed variable $x$를 모델링 합니다.
2) error $\Sigma$
FA는 각 feature가 unique variance를 가진다고 가정합니다.
3) latent variable $s$
$s$를 사용합니다. s가 관찰되었을 때, 데이터 x끼리 independent해집니다. -> conditional independent
FA & EM
latent variable이 존재하므로 EM 알고리즘을 통해 해결해봅시다. (EM알고리즘의 자세한 설명은 이전 포스팅 5.EM 을 참조하세요! )
다시 EM을 복습해보면, E step에서는 latent variable의 posterial distribution $(p(s|x))$을 계산하고, expected complete data log likelihood를 계산합니다. M step에서는 앞서 구한 expected complete data log likelihood를 parameter로 편미분하여, parameter를 업데이트 합니다.

E step에서 posterior distribution을 계산하기 위해서, conditional distribution을 계산하는 Gaussian identity 를 알아야 합니다.
계산 방법을 알려주기 위해 사용된 기호 A와 loading factor을 나타내는 표기 A가 동일하게 A를 사용해서 헷갈리실수도 있지만, 천천히 살펴봐주시면 구분하실 수 있을 겁니다. FA에서 사용하는 실제 값은 파랑색 필기로 적혀져 있습니다.
이 공식을 대입해보면, posterior distibution $p(s|x)$는 다음과 같이 계산됩니다.
$$p(s|x) = N(s|\phi x, I-\phi A), \text{where} \;\; \phi = A^T(AA^T+\Sigma)^{-1}$$
expected complete data log likelihood를 계산하기 위해 필요한 $E\{s_t|x_t\}$, $E\{s_t s_t^T|x_t\}$를 구합니다.


E step
Graphical model 에 따라 complete data log likelihood를 계산합니다. 그리고 앞서 구해둔 sufficient statistics으로 expected complete data log likelihood를 계산합니다.

M step
이제 expected complete data log likelihood를 두개의 parameter $A, \Sigma$로 편미분하여 업데이트합니다.

References
https://towardsdatascience.com/what-is-the-difference-between-pca-and-factor-analysis-5362ef6fa6f9
'ML&DL > Pattern Recognition and Machine Learning' 카테고리의 다른 글
| 5. Expectation Maximization(EM) (1) | 2022.10.25 |
|---|---|
| 4. Clustering (1) | 2022.09.22 |
| 3. Density Estimation (0) | 2022.09.20 |